使用 Canvas 绘制光线飞过效果
经常在一些 Canvas 特效中看到光线飞过的效果,像流星一样拖着长长的尾迹,有时候光线还会沿着曲线运动,如下图的地图中,这种效果是如何实现的呢?今天我们来试着在 Canvas 中实现这种效果。
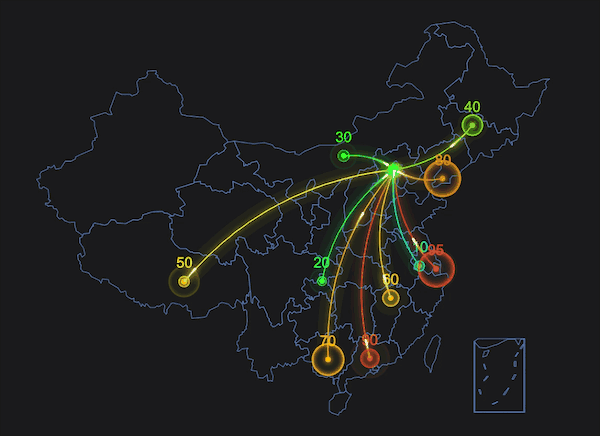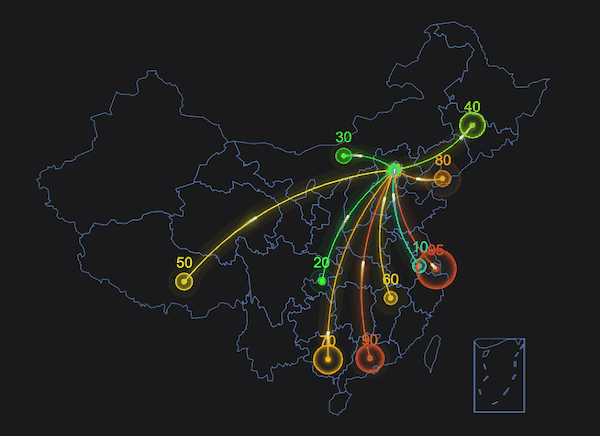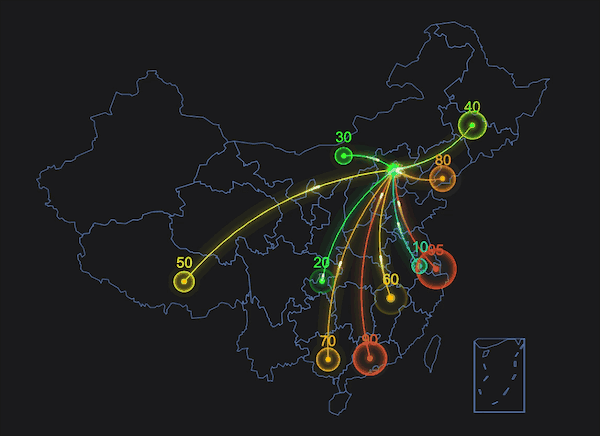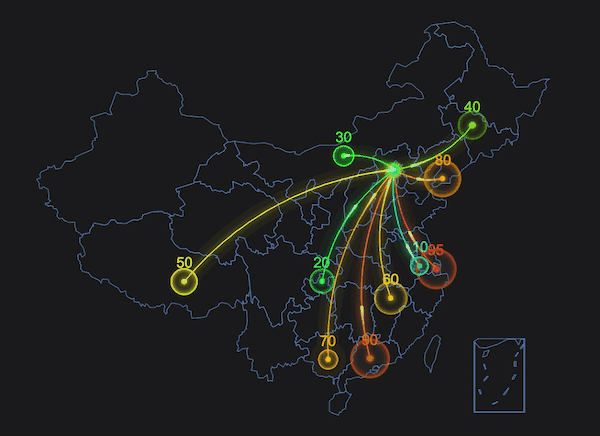
在开始之前,我们先在 html 中创建 Canvas 画布:
<html lang="en">
<head>
<title>canvas 飞线</title>
<style>
body {
margin: 0;
padding: 0;
background: #000000;
}
canvas {
position: absolute;
top: 0;
left: 0;
width: 100%;
height: 100%;
}
</style>
</head>
<body>
<canvas id="mycanvas"></canvas>
<script type="text/javascript">
const mycanvas = document.getElementById("mycanvas");
const context = mycanvas.getContext("2d");
const canvasWidth = window.innerWidth;
const canvasHeight = window.innerHeight;
mycanvas.width = canvasWidth;
mycanvas.height = canvasHeight;
</script>
</body>
</html>
创建 canvas 画布,宽高分别等于屏幕的宽高,为了方便,在之后的内容中,我会略去这部分代码。
绘制光线尾迹

尾迹是光线运动过程中留下的残影,是一个由亮到暗,由粗到细的过程,实际上可以近似的看成逐渐变为透明的一条线,这样可以很容易的用线性渐变实现。
// 创建渐变
function createGradient(context, p0, p1) {
const gradient = context.createLinearGradient(p0.x, p0.y, p1.x, p1.y);
gradient.addColorStop(0, "rgba(255, 0, 255, 0)");
gradient.addColorStop(1, "rgba(255, 0, 255, 1)");
return gradient;
}
p0 和 p1 分别为线段的开始点和结束点,我们使用 moveTo 和 lineTo 绘制直线,并使用已创建好的渐变色来填充直线的路径,需要注意的是,这里的路径不需要闭合。
// 绘制线条
function createLine(p0, p1) {
const gradient = createGradient(context, p0, p1);
context.beginPath();
context.moveTo(p0.x, p0.y);
context.lineTo(p1.x, p1.y);
context.strokeStyle = gradient;
context.lineCap = "round";
context.lineWidth = 3;
context.shadowColor = "rgba(255, 0, 255, 1)";
context.shadowBlur = 5;
context.stroke();
}
实现飞线动画
飞线的运动需要沿着一个方向,我们只需要定义开始点 P0 和结束点 P1 就能确定飞线的运动方向和路径。
const P0 = {
x: 100,
y: 100,
};
const P1 = {
x: 600,
y: 300,
};
我们先假设一个点 p1 在这条直线上运动,p1 随 t 的变化而变化,t 可以是 0 到 1 之间的任意值,给出 t 的值,也就可以求出 p1 的值,公式如下:
x = P0.x + (P1.x - P0.x) * t
y = p0.y + (P1.y - P0.y) * t
利用上面的公式创建一个给出任意 t 值,求对应点坐标的函数:
function computeLinePoint(p0, p1, t) {
return {
x: p0.x + (p1.x - p0.x) * t,
y: p0.y + (p1.y - p0.y) * t,
};
}
因飞线沿着这条直线运动,飞线的起始点和结束点都在这条直线上,我们只需要求出两个点,并将这两个点连结起来,就是飞线。
我们定义两个 t 值,t0 和 t1,分别用来计算飞线的起始点和结束点。为了让飞线有一个从无到有的过程,我们让 t1 > 0.3 以后,t0 的值才开始变化,同样的,在结束的时候,我们要实现飞线从有到无的动画过程,所以需要在 t0 > 0.7 以后,t1 的值等于 1,直到当 t0、t1 在下一次 += 0.005 后都大于 1,重置 t0、t1 的值,动画重新开始。
按照上面的思路创建一个绘制动画的函数:
let t0 = 0; // 飞线起始点的 t 值
let t1 = 0; // 飞线结束点的 t 值
function draw() {
context.clearRect(0, 0, canvasWidth, canvasHeight);
if (t1 < 0.3) {
t0 = 0;
}
if (t0 > 0.7) {
t1 = 1;
}
const startPoint = computeLinePoint(P0, P1, t0);
const endPoint = computeLinePoint(P0, P1, t1);
context.save();
createLine(startPoint, endPoint);
context.restore();
t0 += 0.005;
t1 += 0.005;
if (t0 > 1 && t1 > 1) {
t0 = 0;
t1 = 0;
}
requestAnimationFrame(draw);
}
draw();
到此一个直线飞线效果就实现了,点击查看演示效果。
绘制二次贝塞尔曲线
如何让飞线沿着曲线运动呢,在 canvas 中,绘制曲线的函数主要有两种, 分别是绘制二次贝塞尔曲线的函数 quadraticCurveTo() 和绘制三次贝塞尔曲线的函数 bezierCurveTo(),因为我们要画的是抛物线,所以使用二次贝塞尔曲线。
什么是贝塞尔曲线?
贝塞尔曲线(Bezier curve)是计算机图形学中相当重要的参数曲线,贝塞尔曲线于 1962 年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所发表,他第一个研究了这种矢量绘制曲线的方法,并运用贝塞尔曲线来为汽车的主体进行设计。
贝塞尔曲线(Bezier curve)通过一个方程来描述一条曲线,根据方程的最高阶数,又分为线性贝赛尔曲线,二次贝塞尔曲线、三次贝塞尔曲线和更高阶的贝塞尔曲线。
贝塞尔曲线的定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。
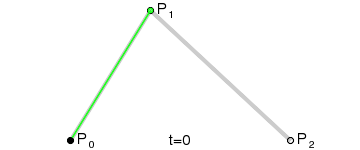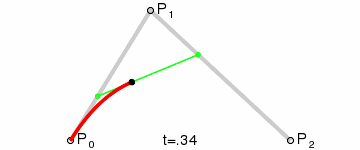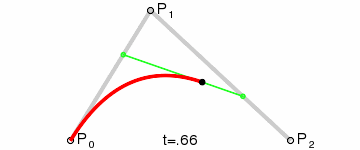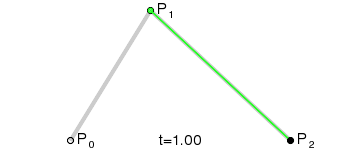
二次贝塞尔曲线方程
二次贝塞尔曲线包括了起始点 P0,终止点 P2,和一个控制点 P1。二次贝塞尔曲线的表达方程如下:
B(t) = (1-t) * (1-t) * P0 + 2 * t * (1-t) * P1 + t * t * P2
其中: t ∈[0,1]
上面的公式可以转化成如下函数
/*!
* 计算二次贝塞尔曲线上的点
* @param {Number} p0 起始点
* @param {Number} p1 控制点
* @param {Number} p2 结束点
* @param {Number} t 当前 t 值, 0 <= t <= 1
* @return {Number} 返回计算后的点
*/
function computeCurvePoint(p0, p1, p2, t) {
return (1 - t) * (1 - t) * p0 + 2 * t * (1 - t) * p1 + t * t * p2;
}
利用这个方程,给出任意 t 值,我们都可以求出曲线上对应点的坐标,让我们先定义三个点,起始点 P0,终止点 P2,和一个控制点 P1。
const P0 = {
x: 100,
y: canvasHeight / 2,
};
const P1 = {
x: canvasWidth / 2,
y: canvasHeight / 2 - 200,
};
const P2 = {
x: canvasWidth - 100,
y: canvasHeight / 2,
};
对于给出任意 t 值,曲线对应点的坐标为:
const currentPoint = {
x: computeCurvePoint(P0.x, P1.x, P2.x, t),
y: computeCurvePoint(P0.y, P1.y, P2.y, t),
};
绘制曲线的片段
沿曲线运动的飞线,其实就是曲线的某一片段,只不过飞线的坐标随 t 的变化而变化,现在我们已经可以求出曲线上点的坐标的集合,只需要把其中某一部分点用 lineTo() 连结起来,就近似的得出了曲线的片段。
// 绘制曲线
function createCurveLine(points) {
const gradient = createGradient(
context,
points[0],
points[points.length - 1]
);
context.beginPath();
context.moveTo(points[0].x, points[0].y);
// 参数 points 是曲线上一部分连续点的集合,我们用 lineTo 把这些点连结起来,就近似的得到了曲线
for (let i = 0; i < points.length; i++) {
const p = points[i];
context.lineTo(p.x, p.y);
}
context.moveTo(points[0].x, points[0].y);
context.strokeStyle = gradient;
context.lineCap = "round";
context.lineWidth = 3;
context.shadowColor = "rgba(255, 255, 0, 1)";
context.shadowBlur = 5;
context.stroke();
}
绘制沿曲线运动的飞线
同样的,按照上面的思路创建一个函数,实现沿曲线运动的飞线效果:
let t0 = 0;
let t1 = 0;
let points = []; // 存储曲线上点的集合
const lineLength = 0.3;
function draw() {
context.clearRect(0, 0, canvasWidth, canvasHeight);
if (t1 < lineLength) {
t0 = 0;
}
if (t0 > 1 - lineLength) {
t1 = 1;
}
const currentPoint = {
x: computeCurvePoint(P0.x, P1.x, P2.x, t1),
y: computeCurvePoint(P0.y, P1.y, P2.y, t1),
};
// 每当 t1 变化时,就将对应的点添加到 points 集合中
points.push(currentPoint);
const len = points.length;
context.save();
if (len > 1) {
createCurveLine(
points.slice(Math.floor(len * t0), Math.max(Math.ceil(len * t1), 2))
);
}
context.restore();
t0 += 0.005;
t1 += 0.005;
if (t0 > 1 && t1 > 1) {
t0 = 0;
t1 = 0;
points = [];
}
requestAnimationFrame(draw);
}
draw();
使用 points.slice 截取集合的一部分,lineLength 的值决定了这部分的大小,最终效果如下图:

完整的代码,你可以在这里查看,也可以点击这里查看演示效果。
结束语
为了便于理解,我没有编写更复杂的代码去优化性能,所以上面的代码有很大的优化空间,由于显示器的分辨率是有限的,曲线上点的集合 points 的密度和曲线的平滑度之间,需要找到一个最佳平衡点,而且 points 也可以缓存起来,不用每次都清空。
利用贝塞尔曲线,还可以为动画添加缓动,我们在写 CSS 动画时用到的 ease, ease-in-out 等就是利用贝塞尔曲线公式求得,有兴趣的话,可以自行了解。
参考
Keywords
canvas 飞线 流星 光线飞过 贝塞尔曲线